Если отнести совет Торо к нашим попыткам изучить Вселенную, то сразу же возникает сложный вопрос: а ведет ли сама Природа свои расчеты на ногте большого пальца? Иными словами -- правят ли окружающим нас миром всего несколько основных законов или же число их бесконечно? Или, быть может, прав известный физик Ричард Фейнман, предположивший, что число главных законов Природы хотя и конечно, но открывать каждый следующий из них становится все труднее и труднее, так что всегда останется место для тайны в поведении Вселенной.

     С этими вопросами тесно связан еще один, а именно: просты или сложны эти главные, основные законы? Большинство биологов, особенно те из них, кто изучает мозг и нервную систему, находятся под сильным впечатлением необыкновенной сложности раскрывающихся перед ними процессов и явлений. Наоборот, большинство физиков сохраняют твердую веру в конечную простоту основных законов Природы -- несмотря на то, что квантовая механика несравненно усложнила их науку, особенно после открытия новых удивительных частиц и видов взаимодействий между ними. Самый лучший пример такого подхода к миру -- взгляд на науку Альберта Эйнштейна. «Наш опыт убеждает нас, -- писал он, -- что природа -- это реализация самых простых математических идей». Когда он выбрал тензорный анализ для того, чтобы с его помощью создать свою теорию гравитации, он взял в руки самый простой инструмент, какой годился для этой работы. Опубликовав свои труды, он как-то сказал о них знакомому, математику Джону Кемени: «Бог ни за что не упустил бы возможность сделать Природу такой простой». Некоторые биографы считают, что огромные научные достижения Эйнштейна связаны с его всегдашним стремлением максимально упростить свою личную жизнь -- вполне в духе советов Торо.

«Спальня Эйнштейна выглядела как монашеская келья, -- писал Питер Майклмор в книге «Эйнштейн, профиль Человека». -- Не было ни картин на стенах, ни ковра на полу... Он часто ходил по дому босиком. Его жена Эльза подрезала ему волосы лишь раз в несколько месяцев -- чаще он не позволял... Он обходился без пижамы, а впоследствии и без носков. «А к чему носки? -- спрашивал он. -- Они только производят дырки». Эльза как-то не в шутку рассердилась  на него, увидев, как он отрезал у только что купленной рубашки рукава ниже локтя. Эйнштейн объяснил ей, что в манжеты надо продевать запонки, а  «это -- пустая трата времени».

«Всякое достояние, -- говорил Эйнштейн, -- это камнь, привязанный к ноге». Кажется, будто эта фраза взята прямо из «Уолдена». Но к ногам Природы, по-видимому, привязано немало камней. Основные ее законы выглядят простыми лишь в первом приближении, и они становятся невероятно сложными, как только приходится обяснять новые наблюдения. Известный философ я математик Альфред Уйтхед писал, что лозунгом каждого ученого должно быть: «Ищи простоту и не верь ей!». Галилео Галилей взял самое простое уравнение для падающих тел, но оно не учитывало некоторых обстоятельств, и потому было заменено несколько более сложным уравнением Исаака Ньютона. Сам Ньютон тоже верил я простоту мнра, «Природа довольствуется простотой, -- писал он, перефразируя Аристотеля, -- и не любит. пышности излишних причин». Тем не менее, уравнения Ньютона, в свою очередь, были подправлены Эйнштейном, а сегодня уже есть физики, которые считают, что и уравнения Эйнштейна тоже необходимо усложнить и модифицировать.

Рискованно утверждать, что раз большинство известных нам основных законов Природы просты, то и пока еще не открытые ее законы тоже будут простыми. Быть может, то, что проще, лежит на поверхности, а в глубинах скрываются вещи, несравненно более сложные?

Наука иногда вдруг резко упрощает наш взгляд на мир, вводя теории, благодаря которым под действие одних и тех же законов подпадают явления, ранее считавшиеся никак между собой не связанными. Так, например, была открыта эквивалентность инерции и тяготения в общей теории относительности. Но, с другой стороны, та же наука иной раз обнаруживает, что за простыми и известными вещами, как, например, структура материи, скрывается никем не ожидаемая сложность. Иоганн Кеплер годами вел борьбу за то, чтобы отстоять выведенные им круговые орбиты планет, потому что окружность -- это простейшая замкнутая кривая. Когда же Кеплер, наконец, убедился, что орбиты эти представляют собой эллипсы, он называл эти эллипсы «навозом», который ему пришлось ввести в астрономию, чтобы избавить ее от еще большего количества навоза. Таким образом получается, что введение дополнительной сложности на каком-то уровне теории может упростить эту теорию в целом.

Простота входит в труд ученого неким мистическим образом -- самая простая и очевидная гипотеза очень часто оказывается и самой правильной. «Самая простая» сказано здесь в некотором объективном смысле. Конечно, всегда существуют какие-то чисто практические аспекты этого вопроса, но они не имеют отношения к существу дела. Если, например, две теории во всем одинаковы, кроме способа выражения (одна, скажем, в метрических мерах, другая -- в традиционных английских величинах), то со стороны ученого нелепо было бы не воспользоваться той, что ему более привычна. Если же две теории не эквивалентны, то есть они ведут к различным предсказаниям, то ученый тоже, естественно, предпочтет проверить первой ту из них, что легче поддается испытанию. Но какую именно -- это зависит от того, какой аппаратурой он располагает, какого рода математика ему более понятна и т. д. Одна и та же теория может казаться простой одному физику и сложной -- другому.

Все подобные субъективные причины не объясняют таинственную роль простоты в научных исследованиях. Почему все-таки при всех прочих равных обстоятельствах верной оказывается именно самая простая гипотеза?

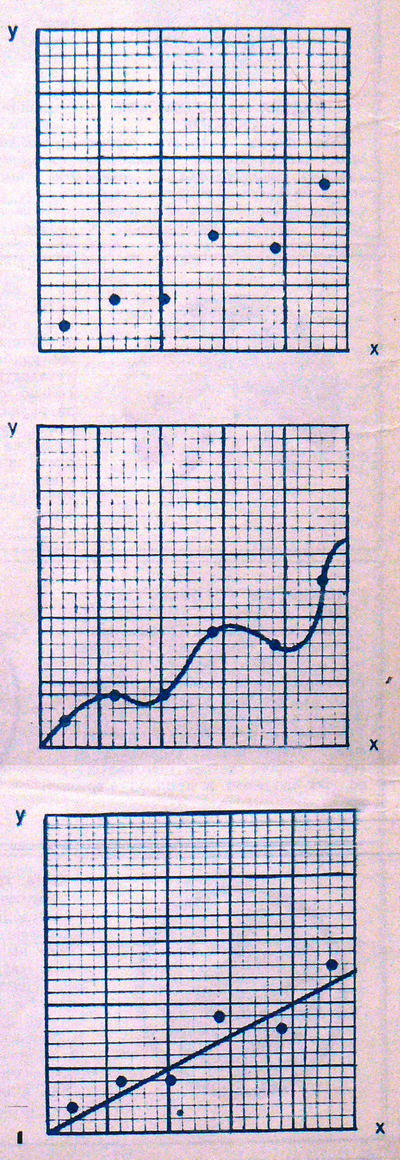
Классический пример -- связь между двумя переменными. Физик отмечает результаты своих наблюдений в виде точек на графике, а затрм соединяет эти точки самой простой кривой, которая «укладывается» на эти точки. Такая кривая -- это, естественно, прямая линия. И здесь простота оказывается даже более важным фактором, чем сами результаты эксперимента! Если точки располагаются близко от прямой линии, то экспериментатор и не подумает соединять точки кривой, проходящей через каждую из них. Он будет считать, что опытные данные получены с некоторой ошибкой и проведет на графике прямую линию, которая не совпадает ни с одной из точек, но зато описывается простым линейным уравнением, например, Х=2У, как на рис. 1.

Если же таким образом не удастся впоследствии предсказать новые наблюдения, то ученый попробует кривую более высокого порядка -- например, параболу или гиперболу. Но при всех прочих равных обстоятельствах более простая кривая имеет больше шансов оказаться правильной -- так устроена Природа. Поразительно большое число ее основных законов выражается уравнениями низких степеней. Общеизвестное стремление Природы к экстремумам -- максимумам и минимумам -- вот еще огромный, ряд примеров ее простоты, потому что, как известно из дифференциального исчисления, функция достигает своего наибольшего илй наименьшего значения, когда ее производная обращается в нуль.

Отсюда вытекает один из самых запутанных вопросов в философии науки; Если существует тот особый тип простоты, который увеличивает вероятность того, что данный закон или теория окажутся верными, то как его, этот тип, определить? А если он может быть определен, то как его измерить?

Ученые стремятся обойти оба эти вопроса. Они интуитивно представляют себе, что такое простота, не заботясь о том, чтобы точно определить это понятие. И в то же время совершенно очевидно, что когда-нибудь способ измерения простоты даст огромный практический эффект. Представим себе, что есть две теории, которые объясняют все известные факты об элементарных частицах. Они равны в своих возможностях предсказать новые наблюдения, хотя предсказания эти различны. Обе теории могут быть правильными. Обе теории могут оказаться ложными. Каждая требует для своей проверки эксперимента. Эксперименты разные, и каждый стоит большую сумму денег. Если простота теории действительно увеличивает вероятность того, что она окажется истинной, то, измерив эту простоту и проведя сначала испытания более простой теории, мы сразу же сэкономим эту большую сумму.

Но сегодня никто не знает, не только как измерить простоту этого типа, но даже и как определить ее. Что-то должно быть сведено к минимуму, но что именно? Конечно же, это не число членов в математической формулировке закона, потому что число это зависит от способа записи: одна и та же формула может записываться с помощью десяти членов в одном виде и включать в себя всего только три члена -- в другом. Знаменитая формула Эйнштейна Е = mс² выглядит такой простой лишь потому, что каждый входящий в нее член -- это сокращенная запись других формул. То же самое встречается и в чистой математике. Например, число «пи» представляет собой тройку с бесконечным рядом десятичных знаков после, запятой. Но мы пишем символ π, который заключает для нас теперь весь этот ряд.

Минимизировать степень, в которой входят в формулу закона различные ее члены, тоже бессмысленно. Например, уравнение первой степени Х=2У лишь в декартовых координатах определяет собой прямую. В полярных координатах то же уравнение описывало бы уже спираль.

Даже сравнивая между собой простейшие геометрические фигуры, мы убеждаемся, что понятие простоты -- совсем не просто. В распространенной серии комиксов «До нашей эры» была картинка, на которой пещерный житель изобрел квадратное колесо. Поскольку в нем слишком много углов и экипаж поэтому слишком сильно трясет, то конструктор возвращается к своей чертежной доске и изобретает «более простое» колесо -- треугольной формы. Число сторон и «встрясок» за один оборот действительно сведено минимуму, но изобретатель ушел еще дальше от в самом деле простейшего колеса -- круга, у которого вовсе нет углов. Или же нам следует считать круг самым сложным из возможных колес, поскольку он представляет собой многоугольник с бесконечным числом углов? Равносторонний треугольник проще, чем квадрат в том смысле, что у него меньше сторон и углов. Но, с другой стороны, квадрат проще треугольника, если нам важно, чтобы в формуле для вычисления площади фигуры было как можно меньше членов. Таким образом вопрос о том, что же такое простота, остается открытым и запутанным.

Один из наиболее соблазнительных путей оценивать простоту гипотезы, выраженной, словами, -- подсчитывать число входящих в нее примитивных понятий. Но и этот путь, к несчастью, ведет в тупик -- можно искусственно уменьшить число таких понятий, объединяя их друг с другом. Это ярко показывает философ Нельсон Гудман в своем знаменитом «зелубом» парадоксе, о котором написаны уже многие десятки научных статей. Парадокс Гуд мана заключается в следующем. Дан простой закон: ВСЕ ИЗУМРУДЫ ЗЕЛЕНЫЕ. Теперь введем новое понятие -- «зелубой». Оно означает способность быть зеленым до, скажем, 1 января 1972 года и быть голубым после этого срока. Мы теперь утверждаем второй закон: ВСЕ ИЗУМРУДЫ ЗЕЛУБЫЕ.

Оба закона включают в себя равное число понятий. Оба объясняют все наблюдаемые факты. У обоих одинаковая «предсказательная сила». Если в дальнейшем будет найден хоть один изумруд необычного цвета, то этот камень погубит сразу оба закона. И все-таки всякий предпочтет первый закон, потому что понятие «зеленый» проще, чем «зелубой» -- оно не требует новых теорий, чтобы объяснить внезапную смену цвета изумрудов 1 января 1972 года.

Хотя в этом частном аспекте проблемы простоты Гудман сделал больше, чем кто бы то ни было, он все еще далек от конечных результатов. А что же тогда сказать о куда более трудной задаче измерения не частной, а общей простоты закона или теории? Поистине, понятие простоты в науке невероятно сложно! Может оказаться, что в Природе существует не один вид простоты, а несколько, и каждый из них необходимо оценить и учесть, высчитывая общую простоту гипотезы.

И в чистой математике, тсак это ни удивительно, возникают подобные же затруднения. Математики ищут новую теорему порой почти так же, как физики ищут новый закон -- они производят, эксперимент. Рисуя карандашом один за другим различные четырехугольники -- а это вполне аналогично экспериментированию с физическими моделями -- геометр, может обнаружить, что, когда он рисует квадраты на внешних сторонах четырехугольника, то линии, соединяющие центры противоположных квадратов, оказываются равными и пересекаются под углом в 90 градусов (см. рис. 2).

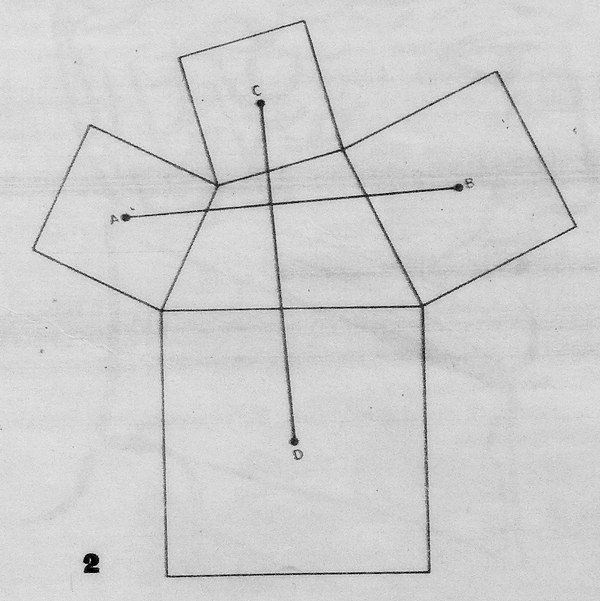
Он экспериментирует с четырехугольниками различной формы и всегда получает один и тот же результат. Теперь он уже чувствует запах новой теоремы. Как и физик в подобной же ситуации, он выдвигает простейшую гипотезу. Он не проверяет для начала правильность теоремы, о том, что отношение длин этих линий равно, например, 1,0002 и что они пересекаются под углом в 89 или 91 градус -- хотя при тех грубых способах измерений, какими он обладает, он вполне мог бы получить эти цифры. Нет, математик вначале проверяет более простое предположение -- свою догадку, что линии перпендикулярны и равны. Его «проверка» в отличие от эксперимента, который поставил бы физик, состоит в том, чтобы найти дедуктивное доказательство, которое превратило бы его гипотезу в безусловно истинное высказывание. Одно из таких доказательств приведено в книге И. М. Яглома «Геометрические преобразования».

Комбинаторика богата подобными примерами, когда простейшая догадка оказывается правильной. Но, как и в окружающем нас мире, в этой науке тоже встречаются сюрпризы. Чтобы убедиться в этом, попробуйте решить следующую задачку. В произвольном месте на окружности расположено две или больше точек. Каждая пара точек соединяется прямой, как показано на рис. 3.

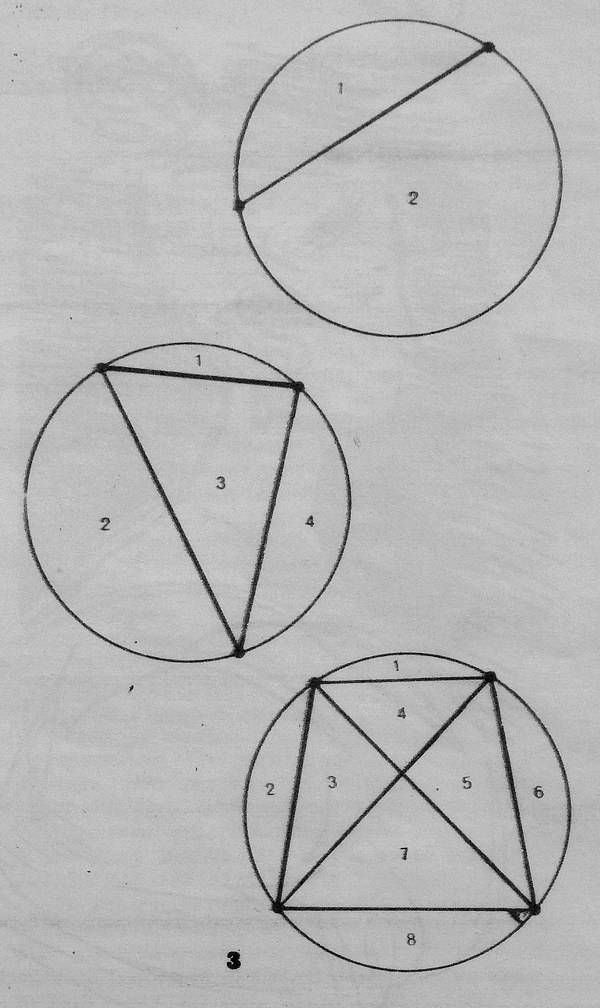
Вопрос звучит так: если на окружности п точек, то на сколько участков разобьется круг соединяющими их прямыми? На рисунке видно, что для двух точек таких участков 2, для трех -- 4, для четырех -- 8. Сколько их будет для пяти, шести и вообще для любого числа точек на окружности?

И, наконец, в заключение простенькая задачка, задача-шутка. Придумайте, как самым простым способом вскипятить яйцо в течение 15 минут, если у вас под рукой двое песочных часов -- семи- и одиннадцатиминутные?